原文:https://www.cs.helsinki.fi/group/goa/mallinnus/lines/bresenh.html
基本Bresenham算法
考虑在光栅网格上绘制一条直线,这条直线的斜率是 $0\leq m \leq 1$。
斜率定义:假设直线起点是(x1, y1),终点是(x2, y2),则斜率=(y2-y1)/(x2-x1)。
如果我们进一步限制该绘制程序,使其在绘制时 x 值不断递增,那么很明显,在 (x, y) 处绘制一个点后,直线下一个点的位置范围非常有限:
- 可以是 (x+1, y),
- 或者是 (x+1, y+1)。
所以,在平面的第一个八分之一区域画线,变成了每一步进行一次二选一的问题。
我们可以画出绘图程序在绘制 (x, y) 时发生的情况。
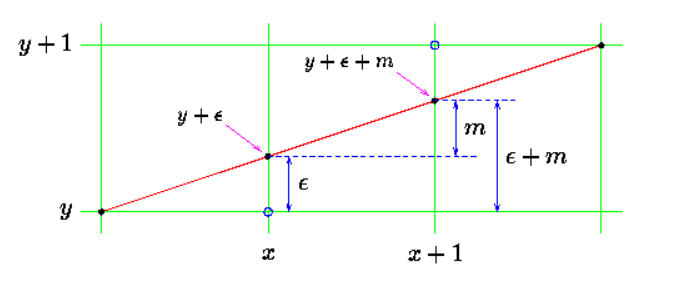
在绘制 (x, y) 时,通常情况下,直线上实际的数学点和像素网格不是一一对应的,绘制的点会有误差,绘制程序需要在绘制位置和屏幕实际分辨率之间做出折中。所以我们把每个 y 坐标和一个误差值 $\epsilon$ 联系起来,y的实际值应该是 $y + \epsilon$。此误差值范围为 -0.5 到 +0.5。
从 x 移动到 x+1 时,让 y 坐标的值增加一个等于直线斜率 m 的量,如果这个新值与 y 之间的差小于 0.5,我们将绘制 (x+1, y),否则绘制 (x+1, y+1)。很明显,通过这样做,可以将数学线段和实际绘制线段之间的总误差降到最小。
把这个新点产生的误差写回到 $\epsilon$,就可以在 x+2 处对下一个点重复整个过程。
新的误差值可以采用两个可能值中的一个,具体取决于绘制的新点。如果选择(x+1,y),新的误差值是:
$\epsilon_{new}$ <--- $(y+\epsilon+m)-y$
否则是:
$\epsilon_{new}$ <--- $(y+\epsilon+m)-(y+1)$
这种方法通过误差变量 $\epsilon$ 来控制绘图,使DDA算法避免了舍入操作。
DDA的全称是Digital Differential Analyzer,即数值微分算法,是一种最简单的画直线算法。
$\epsilon$ <--- 0,y <--- $y_1$ For $x$ <--- $x_1$ to $x_2$ do Plot point at $(x, y)$ If $(\epsilon+m<0.5)$ $\epsilon$ <--- $\epsilon+m$ Else $y$ <--- $y+1$,$\epsilon$ <--- $\epsilon+m-1$ EndIf EndFor 这里使用了浮点值。但是,如果我们将绘图测试的两边乘以$\Delta{x}$,然后再乘以2,会发生什么情况: $\epsilon+m<0.5$ $\epsilon+\Delta{y}/\Delta{x}<0.5$ $2\epsilon\Delta{x}+2\Delta{y}<\Delta{x}$ 这个不等式中的所有量现在都是整数。 用 $\epsilon^'$ 代替 $\epsilon\Delta{x}$,变成: $2(\epsilon^'+\Delta{y})<\Delta{x}$ 到这为止,通过整数计算,就能决定绘制哪个点了。 上面伪码中误差值的更新规则也可以用 $\epsilon^'$ 表示,浮点数版本如下: $\epsilon$ <--- $\epsilon+m$ $\epsilon$ <--- $\epsilon+m-1$ 两边都乘以 $\Delta{x}$: $\epsilon\Delta{x}$ <--- $\epsilon\Delta{x}+\Delta{y}$ $\epsilon\Delta{x}$ <--- $\epsilon\Delta{x}+\Delta{y}-\Delta{x}$ 转换成 $\epsilon^'$ 形式: $\epsilon^'$ <--- $\epsilon^'+\Delta{y}$ $\epsilon^'$ <--- $\epsilon^'+\Delta{y}-\Delta{x}$ 最后,使用这个新的误差值 $\epsilon^'$,结合上面的变换过程,可以得到Bresenham的纯整数画线算法: $\epsilon^'$ <--- $0$, $y$ <--- $y_1$ For $x$ <--- $x_1$ to $x_2$ do Plot point at ($x$, $y$) If $(2(\epsilon^'+\Delta{y})<\Delta{x})$ $\epsilon^'$ <--- $\epsilon^'+\Delta{y}$ Else $y$ <--- $y+1$,$\epsilon^'$ <--- $\epsilon^'+\Delta{y}-\Delta{x}$ EndIf EndFor
- 仅整数-因此高效(快速)。
- 乘2可以用左移实现。
- 此版本仅限于第一个八分之一平面,斜率:$0\leq m \leq 1$。
以下是这个算法的C++实现:
void linev6(Screen & s,
unsigned x1, unsigned y1,
unsigned x2, unsigned y2,
unsigned char colour)
{
int dx = x2 - x1,
dy = y2 - y1,
y = y1,
eps = 0;
for (int x = x1; x <= x2; x++ ) {
s.Plot(x, y, colour);
eps += dy;
if ((eps << 1) >= dx) {
y++; eps -= dx;
}
}
}
这是一个全整数函数,使用左移位进行乘法,并通过巧妙地使用eps变量来消除冗余操作。
不过,这个Bresenham算法的实现还不完整,它没有检查参数的有效性。而且,实际的实现不仅仅只适用于斜率在第一个八分之一平面的直线,而是应该能处理任意斜率的直线。