JavaScript实现软件光栅化渲染器02-如何画直线

项目代码：https://github.com/foupwang/JavaScript3DRenderer
开发环境：VSCode+Chrome浏览器
参考：《Windows游戏编程大师技巧》(第2版) /《3D游戏编程大师技巧》（André LaMothe）

前文介绍了画点函数，本文说明如何绘制直线。

在计算机屏幕上画直线碰到的第一个问题是：由于屏幕是一个由整数坐标表示的2D网格，因此要在屏幕上显示类似 (20.5, 30.3) 的点几乎是不可能的，只能采用近似值，例如，把点显示为 (20, 30) 。或者采用较高级的算法，通过带权像素绘制出围绕 (20.5, 30.3) 、具有不同像素浓度的一系列点来代替这一点。

光栅化基础

把像素以最接近实际直线的位置从点 P0 到 P1 进行填充，这个过程称为光栅化。

要理解光栅化的原理，先来温习一下斜率的定义。直线的斜率同直线与x轴的夹角有关。如果一条直线的斜率为0，则该直线为水平直线；如果斜率为无穷大，则直线为垂直直线；如果斜率为1，则为45度的对角斜线。斜率的定义为单位前进距离的上升量，数学表达式为：

斜率(m) = 上升/下降 = y方向的改变/x方向的改变 = dy/dx = (y2-y1)/(x2-x1)

例如：一条直线通过点 P0(1, 2) 和点 P1(5, 22)，则该直线的斜率m = (22-2)/(5-1) = 5.0。那么，斜率5.0到底意味着什么呢？它意味着x坐标每增加1.0个单位，y坐标就相应增加5.0个单位。这就是光栅化算法的基础。所以，画一条直线的大致流程是：
1、计算斜率m；
2、画点(x, y)；
3、在x方向每前进1.0个单位，就在y方向相应前进m个单位，把这两个值加到(x, y)上；
4、重复2-4步，直到完成。
下图给出了点P0（1，2）到点P1（5，22）绘制的示意图。

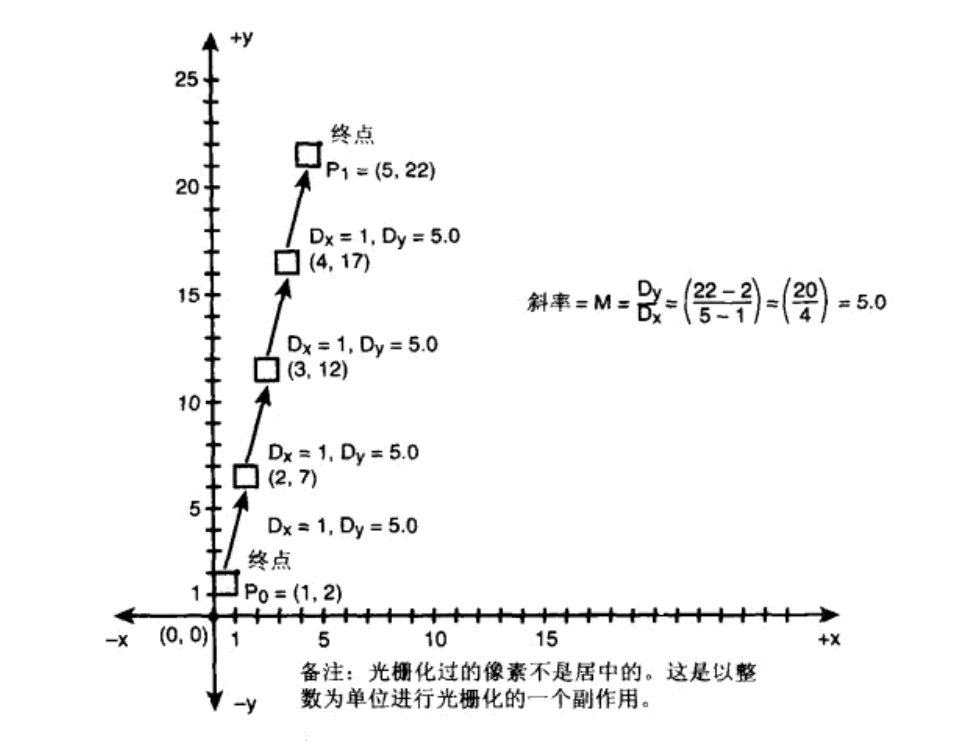
看出问题在哪了吗？这样画的不是一条连续的线，因为有许多空洞。只要x还是一个整数，就会出现这样的问题。其实无论你采取多小的x步长，用斜率计算还是会出现遗漏的点。因此不得不采用其它方法，这就是Bresenham算法的基础。

Bresenham算法

Bresenham是由Bresenham在1965年发明的，最初是为了在绘图仪上画线而设计，后来被运用于计算机图形学。

简单地说，Bresenham算法开始于 (x0, y0) 点，但是不采用斜率计算移动。它先在x方向移动一个像素，然后再决定如何移动y方向的像素，使所绘制的直线尽量接近于实际的线。这是通过使用一个衡量光栅化直线与实际直线之间的接近程度的误差项来实现的，该算法对误差项不断调整，使得光栅线能够尽量接近真实的直线。

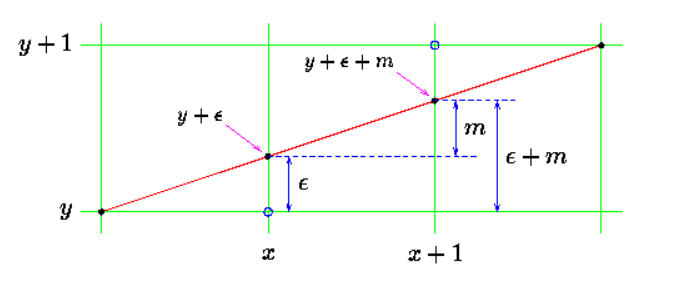
如上图所示，当前为 (x, y+ε)，下一个要绘制的点为 (x+1, y+ε+m)，可以看出，当 (ε+m) < 0.5 时，绘制 (x+1, y) 点；否则绘制 (x+1, y+1) 点。每次绘制后，ε 更新为新值。算法伪代码如下：

ε = 0, y = y1
for (x=x1; x<=x2; x++) {
  drawPoint(x, y);
  if ((ε+m) < 0.5) {
    ε = ε + m;
  } else {
    y++, ε = ε + m - 1;
  }
}

这是浮点数版本。现在把两边都乘以dx，再乘以2，得到整数版本如下：

ε = 0, y = y1;
for (x = x1; x <= x2; x++) {
  drawPoint(x, y);
  if (2*(ε+dy) < dx) {
    ε = ε + dy;
  } else {
    y++, ε = ε + dy - dx;
  }
}

再稍加变换优化，完整如下：

dx = x2 - x1;
dy = y2 - y1;
y = y1;
eps = 0;
for (int x = x1; x <= x2; x++) {
  drawPoint(x, y);
  eps += dy;
  if ((eps << 1) >= dx) {
    y++, eps -= dx;
  }
}

这就是Bresenham算法的核心实现，详细的论述和推导过程可参见我的另一篇文章：Bresenham快速画直线算法(中文翻译+注释)

最终实现的实例程序，可用浏览器打开 ch02/DrawLine.html 查看。